Classwork 3

Property Rights, the Coase Theorem, and the Environment

Question 1. Property Rights and Coasian Bargaining

Consider a society with just two people. Person 1 enjoys playing loud music for \(h\) hours, while Person 2 dislikes the noise. Both are self-interested and care only about their own payoff.

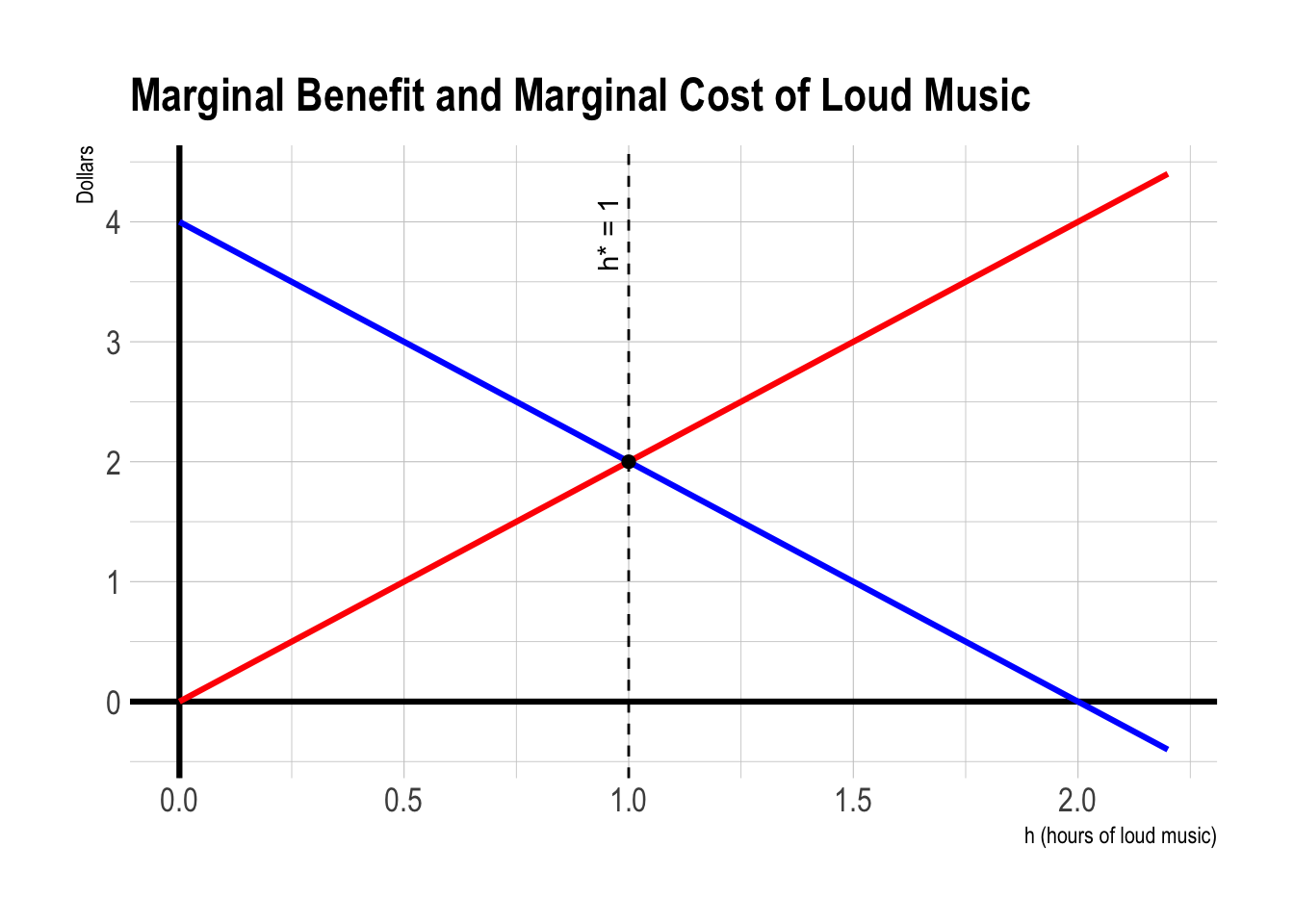
• Person 1’s marginal benefit (in dollars) from music is:
  \(MB(h) = 4 - 2h\).
  
• Person 2’s marginal cost (in dollars) from music is:
  \(MC(h) = 2h\).

Note

Here, \(MB(h)\) and \(MC(h)\) are functions of \(h\).
Transfers \(T\) (in dollars) are lump-sum payments between the two people.

a. Market outcome

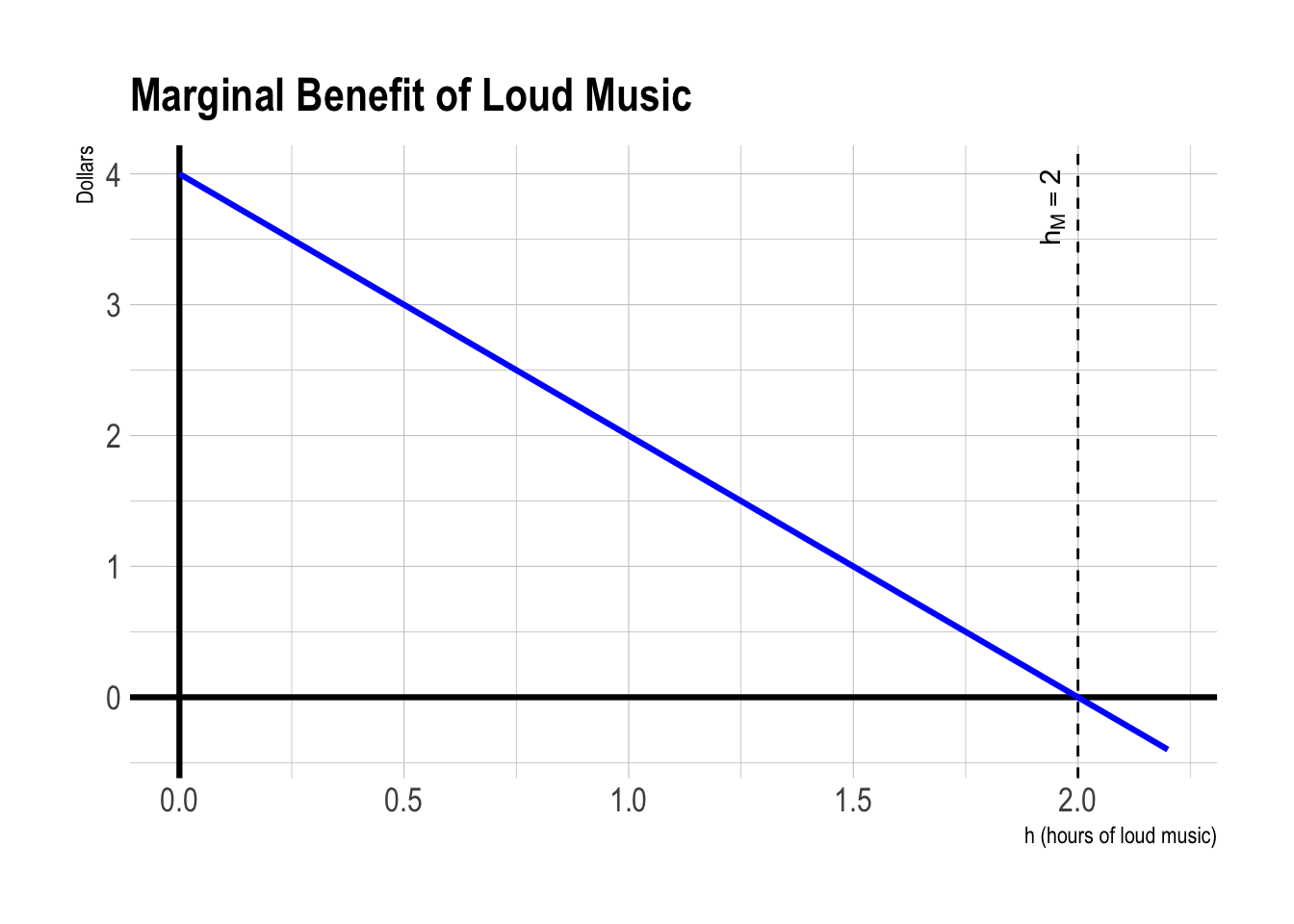
If the decision is left entirely to Person 1, what level of music \(h_M\) will she choose? Why?

Show answer

Person 1 chooses \(h\) to maximize her own payoff and ignores Person 2’s cost.
She sets \(MB(h)=0\):
\[ 4-2h=0 \;\;\Rightarrow\;\; \boxed{h_M=2}. \]

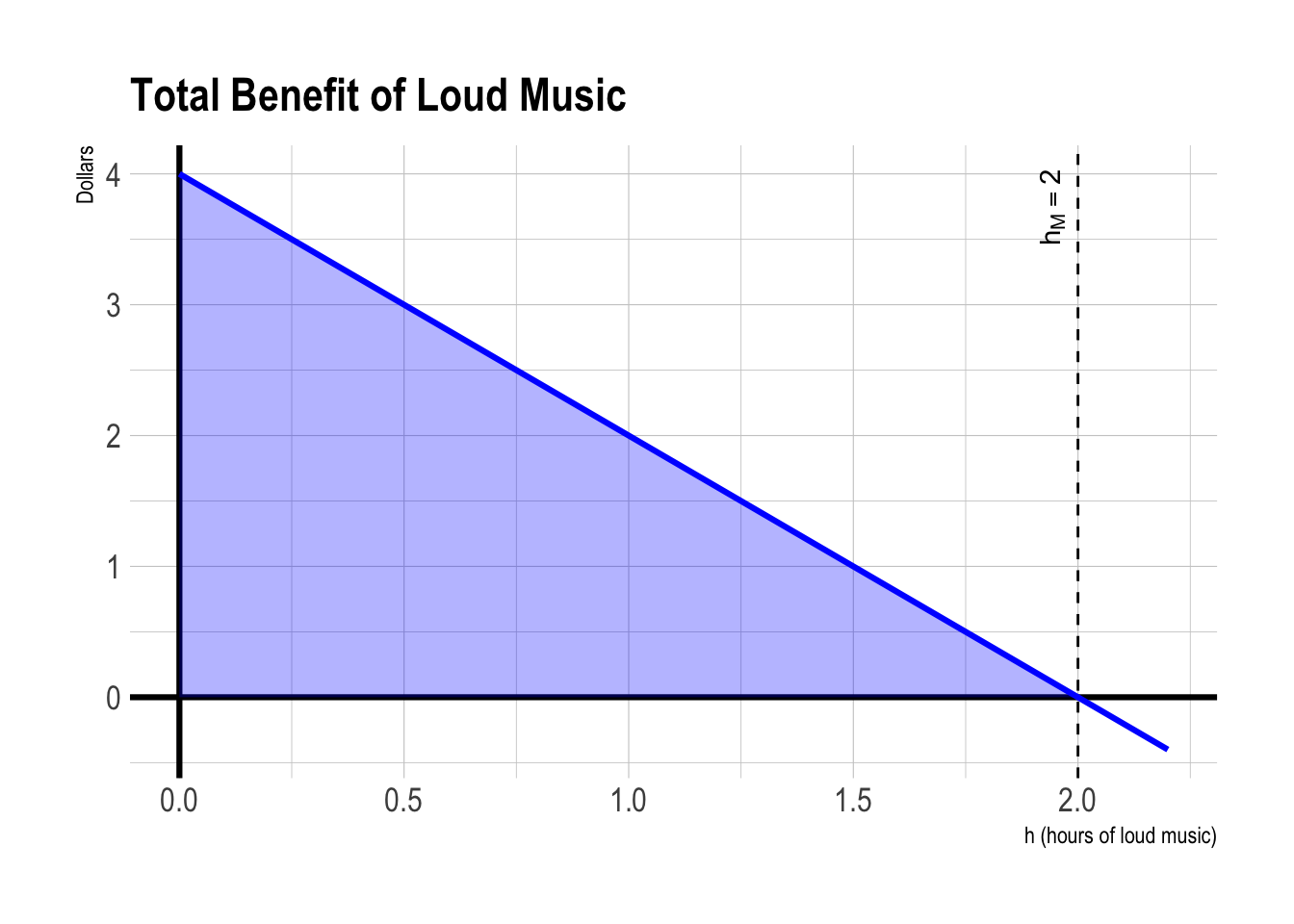
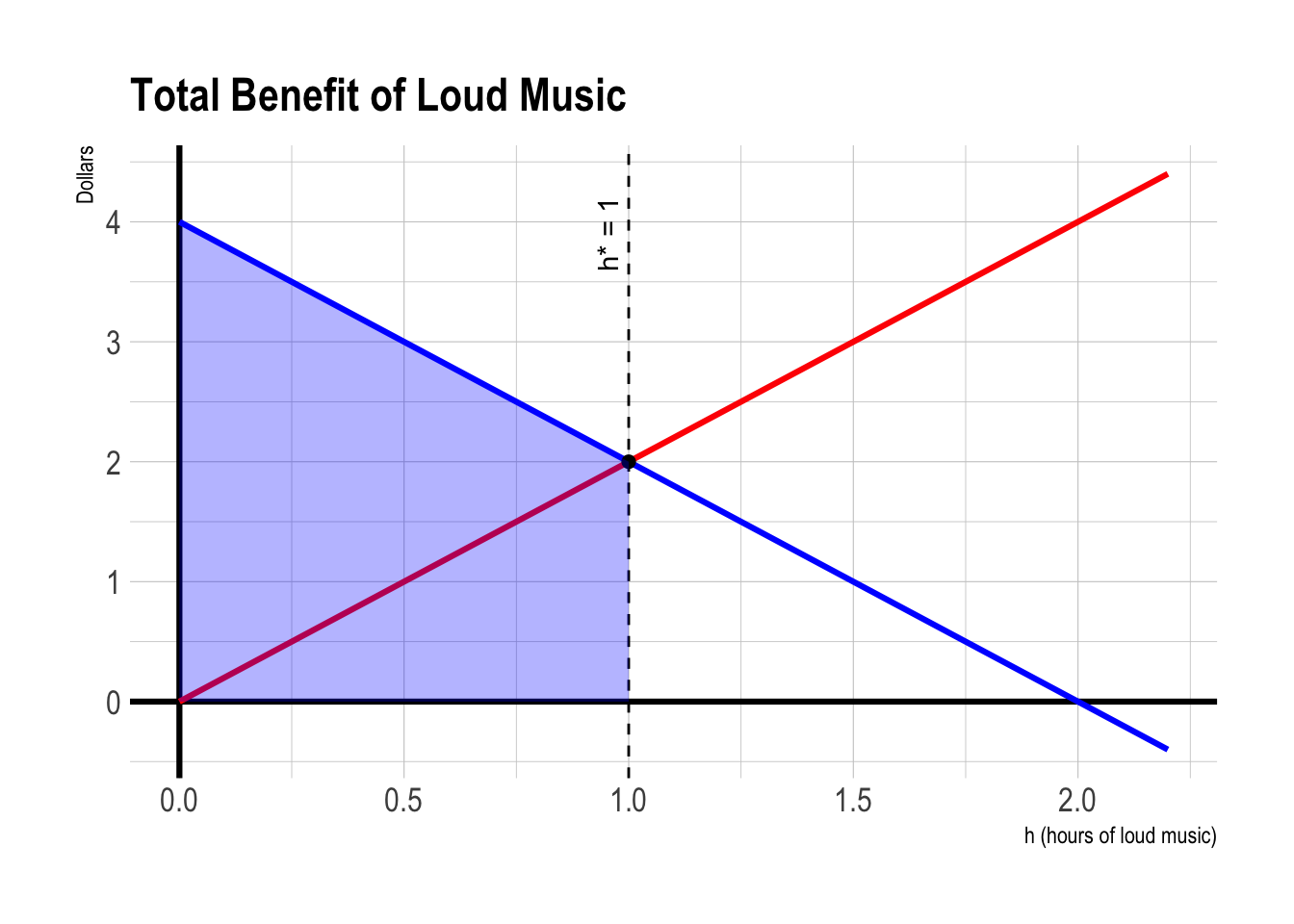
Total benefit (\(TB\)) is the area under the \(MB\) curve. So, total benefit is maximized at \(h=2\).

Why? With no private cost, she keeps increasing \(h\) until her marginal benefit hits zero; the neighbor’s harm is not internalized.

Examples

• At \(h=0\): Total benefit of playing music is zero.

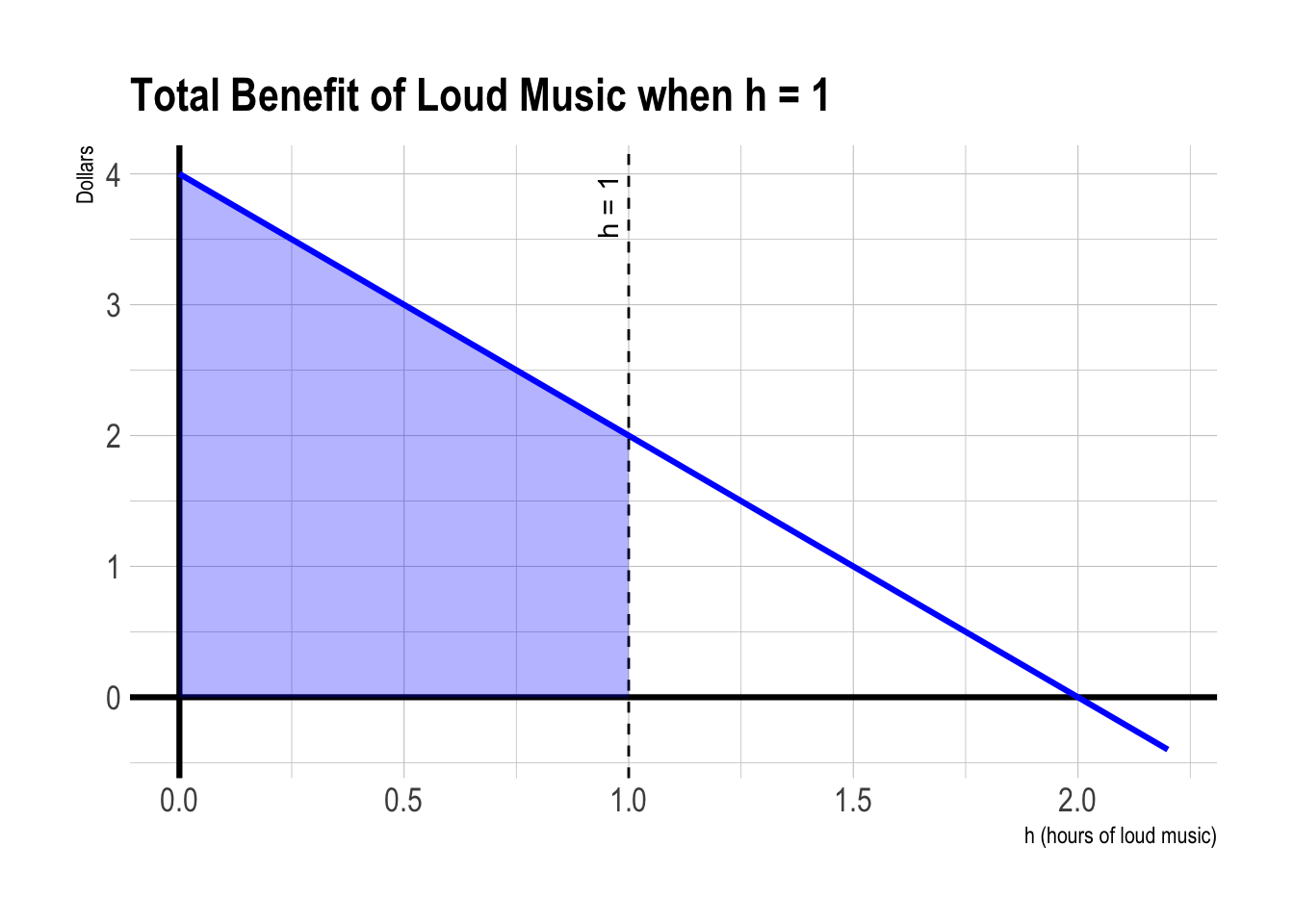
• At \(h=1\): Total benefit is smaller than the above:

b. Socially efficient outcome

What is the socially optimal level \(h^{*}\)? Why?

Show answer

Efficiency requires \(MB(h)=MC(h)\), so that social welfare (total surplus) is maximized:

\[ 4 - 2h = 2h \;\;\Rightarrow\;\; \boxed{h^* = 1}. \]

Why? At \(h=1\), the next unit’s benefit equals the next unit’s cost, so total surplus is maximized:

\[ TS(h) = TB(h) - TC(h), \]

which peaks at \(h=1\).

• When \(MB > MC\) (for \(h < 1\)): the next unit of music adds more benefit than harm, so playing more music increases the total surplus.
  
• When \(MB < MC\) (for \(h > 1\)): the next unit of music causes more harm than benefit, so playing more music shrinks the total surplus.
  
• Only when \(MB = MC\) (at \(h=1\)) do we stop, because any movement in either direction would reduce total surplus.

The total surplus of loud music is the triangle area below:

This is because the total benefit is the area under the MB, and the total cost is the area under the MC:

• Total benefit (\(TB\)) from 1 hour of loud music

• Total cost (\(TC\)) from 1 hour of loud music

c. Person 1 has the right to play

Suppose the government gives Person 1 the legal right to play as much as she wants (\(h=h_M\)).
Person 2 may then “bribe” Person 1 to reduce music in exchange for a lump-sum transfer \(T\) (in dollars).
Assume there are no transaction costs in bargaining.

• Show how bargaining can still lead them to agree on the socially optimal level \(h^{*}\).
  • Identify the possible range of transfers \(T\) (in dollars), paid from Person 2 to Person 1, that makes both better off compared to their initial legal entitlement (\(h=h_M, T=0\)).

Show answer

Starting from \(h=2\), \[ MC(2)=4>MB(2)=0, \]

so both gain by reducing \(h\) until \(MB=MC\), i.e., to \(\boxed{h^{*}=1}\).

Transfers to cut noise from \(2\to 1\):

• Person 2 should be better off from the bargaining.
  • This means that Person 2’s total cost (harm from music plus any transfer paid to Person 1) at \(h=1\) with transfer \(T\) must be no greater than at the initial entitlement \(h=2\) with \(T=0\).

\[ \begin{align} TC(h=1) + T &\;\leq\; TC(h=2) \qquad \Leftrightarrow\\ \left(\frac{1}{2}\times 1 \times 2\right) + T &\;\leq\; \frac{1}{2}\times 2 \times 4 \qquad \Leftrightarrow\\ 1 + T &\;\leq\; 4\qquad \Leftrightarrow\\ T&\;\leq\; 3 \end{align} \]

• Person 1 should also be better off from the bargaining.
  • This means that Person 1’s net payoff (the benefit from music plus any transfer received) at \(h=1\) with \(T\) must be at least as high as at the initial entitlement \(h=2\) with \(T=0\).

\[ \begin{align} TB(h=1) + T &\;\geq\; TB(h=2) \qquad \Leftrightarrow\\ \left(\frac{1}{2}\times (4 + 2) \times 1\right) + T &\;\geq\; \frac{1}{2}\times 2 \times 4 \qquad \Leftrightarrow\\ 3 + T &\;\geq\; 4\qquad \Leftrightarrow\\ T&\;\geq\; 1 \end{align} \] Therefore, any transfer \(T\) with \[ 1\;\leq\; T \;\leq\; 3 \] paid from Person 2 to Person 1 makes both (weakly) better off.

d. Person 2 has the right to silence

Now suppose the government gives Person 2 the legal right to silence (\(h=0\)).
Person 1 may then “bribe” Person 2 to allow some music in exchange for a lump-sum transfer \(T\) (in dollars).
Assume there are no transaction costs in bargaining.

• Show how bargaining can still lead them to agree on the socially optimal level \(h^{*}\).
  • Identify the possible range of transfers \(T\) (in dollars), paid from Person 1 to Person 2, that makes both better off compared to their initial legal entitlement (\(h=0, T=0\)).

Show answer

Starting from \(h=0\), \[ MC(0)=0<MB(0)=4, \]

so both gain by increasing \(h\) until \(MB=MC\), i.e., to \(\boxed{h^{*}=1}\).

Transfers to increase noise from \(0\to 1\):

• Person 2 should be better off from the bargaining.
  • This means that Person 2’s net payoff (transfer received from Person 1 minus the harm from music) at \(h=1\) with transfer \(T\) must be at least as great as under the initial entitlement \(h=0\) with \(T=0\).

\[ \begin{align} T - TC(h=1) &\;\geq\; -TC(h=0) \qquad \Leftrightarrow\\ T - \left(\frac{1}{2}\times 1 \times 2\right) &\;\geq\; 0 \qquad \Leftrightarrow\\ T &\;\geq\; 1 \end{align} \]

• Person 1 should also be better off from the bargaining.
  • This means that Person 1’s net payoff (the benefit from music minus any transfer paid to person 2) at \(h=1\) with \(T\) must be at least as high as at the initial entitlement \(h=0\) with \(T=0\).

\[ \begin{align} TB(h=1) - T &\;\geq\; TB(h=0) \qquad \Leftrightarrow\\ \left(\frac{1}{2}\times (4 + 2) \times 1\right) - T &\;\geq\; 0 \qquad \Leftrightarrow\\ 3 &\;\geq\; T \end{align} \] Therefore, any transfer \(T\) with \[ 1\;\leq\; T \;\leq\; 3 \] paid from Person 1 to Person 2 makes both (weakly) better off.

Why transfers don’t justify stopping at \(h = 0.5\) or \(h = 1.5\)?

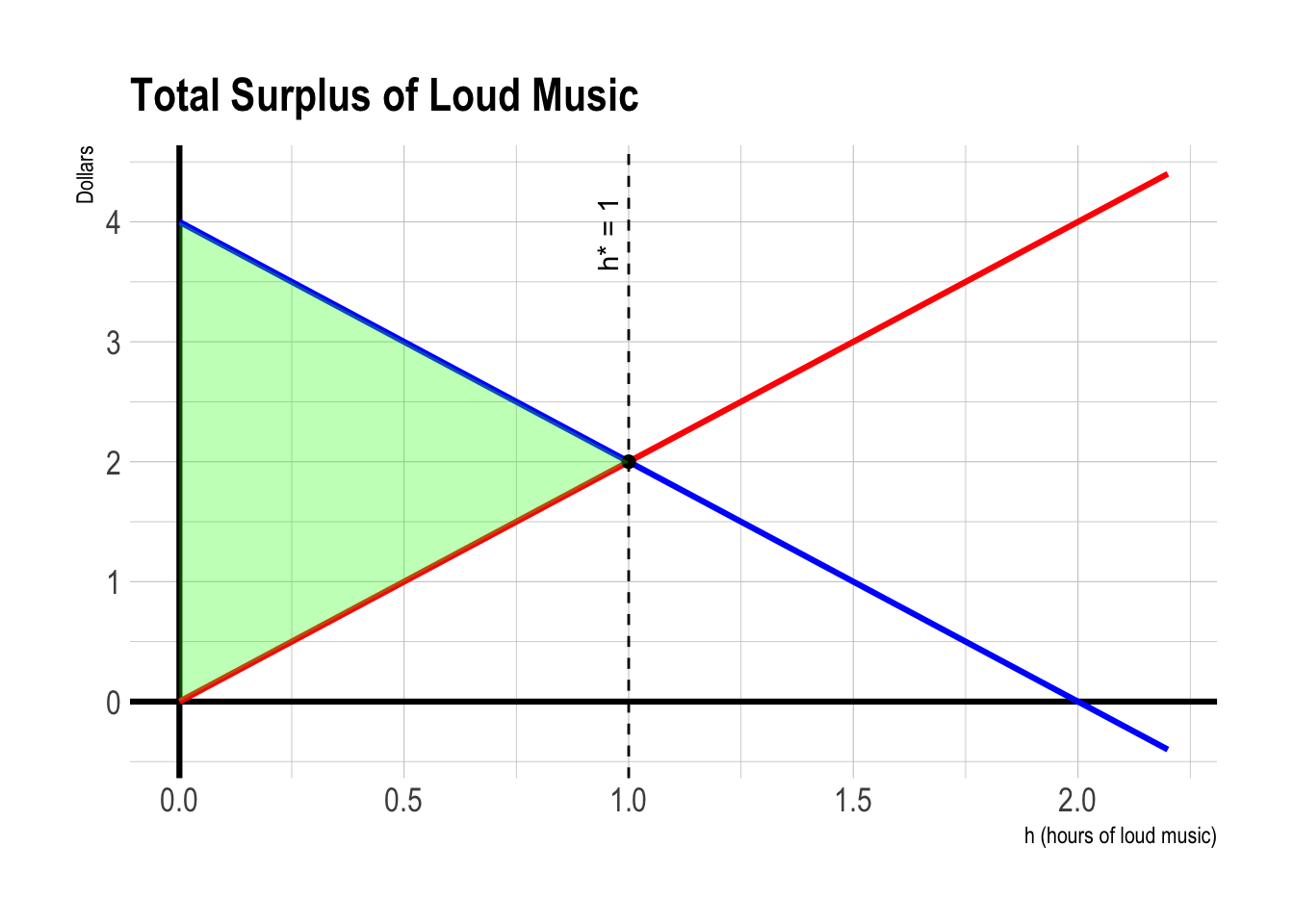
• The total pie from bargaining is the total surplus—the total dollar value created, equal to Person 1’s total benefit from music minus Person 2’s total harm.
  • Intuitively, the total surplus represents the size of the pie before deciding how to slice it between the two people.
    
  • We call it a “pie” because it measures the overall gains available from negotiation: the larger the pie, the more there is for the two to share, even though bargaining determines who gets which slice.

\[ TS(h) = TB(h) - TC(h) \]

• Lump-sum transfers (\(T\)) only redistribute this surplus between the two people; they don’t create or destroy it.

• If Person 1 has the right to play:
  \[ (\text{Total Pie}) = (TB(h) + T) - (TC(h) + T) = TS(h) \]

• If Person 2 has the right to silence:
  \[ (\text{Total Pie}) = (TB(h) - T) - (TC(h) + T) = TS(h) \]

• At \(h=0.5\), some surplus is left unclaimed. Moving closer to \(h=1\) makes the pie larger.
  

• At \(h=1.5\), some surplus is left unclaimed. Cutting back toward \(h=1\) makes the pie larger.

• Intuition:

  • When \(MB > MC\) (\(h < 1\)), the next unit of music adds more benefit than harm, so the pie grows.
    
  • When \(MB < MC\) (\(h > 1\)), the next unit causes more harm than benefit, so the pie shrinks.
    
  • Only when \(MB = MC\) (\(h=1\)) is the pie maximized; any movement away reduces total surplus.

Numerical Illustration of the Total Pie

\(h\)	\(TS(h)\) (in $)
0.5	\(1.5\)
1.0	\(2.0\)
1.5	\(1.5\)

The total surplus (“pie”) is maximized at \(h^* = 1\) with \(TS = 2\).

Conclusion: Regardless of how the pie is sliced (the transfer \(T\)), the pie itself is largest only at \(h^{*}=1\).

Note

How the pie is divided—that is, the actual transfer size—depends on the relative bargaining power of the two parties in a given situation.