Week 6

Common Property Resources and Public Goods

In Week 6, we will discuss the economics of common pool resources and public goods.

🏫 Lecture Slides

• Lecture 6 - Common Property, Open Access, and Property Rights
  View Slides

• Lecture 7 - Public Goods
  View Slides

🎥 Looking for lecture recordings? You can only find those on Brightspace.

✍️ Classwork

• Classwork 4: Common Pool Resources
  📄 View Classwork

📝 Homework

🏡 Homework 2 has been posted. 🏡

📚 Recommended Reading

Economics of Public Goods

Markets usually coordinate private goods well through supply and demand. Public goods are different. The usual market logic breaks down—not because firms can’t produce them, but because people have weak incentives to reveal how much they value them.

Why markets underprovide public goods

For a private good, your demand curve reflects both your marginal benefit (MB) and your willingness to pay (WTP). If a shirt gives you $30 of benefit, you’ll pay up to $30.

For a public good, those diverge: you still enjoy the benefit whether or not you contribute, so WTP is typically below MB. That gap—driven by free-riding—means voluntary contributions fall short of the efficient level.

This is a demand-side failure. (Contrast with open-access fisheries, where the failure is on the production side: too many boats, too much effort, resource overuse.)

A two-person example: Doug and Sasha

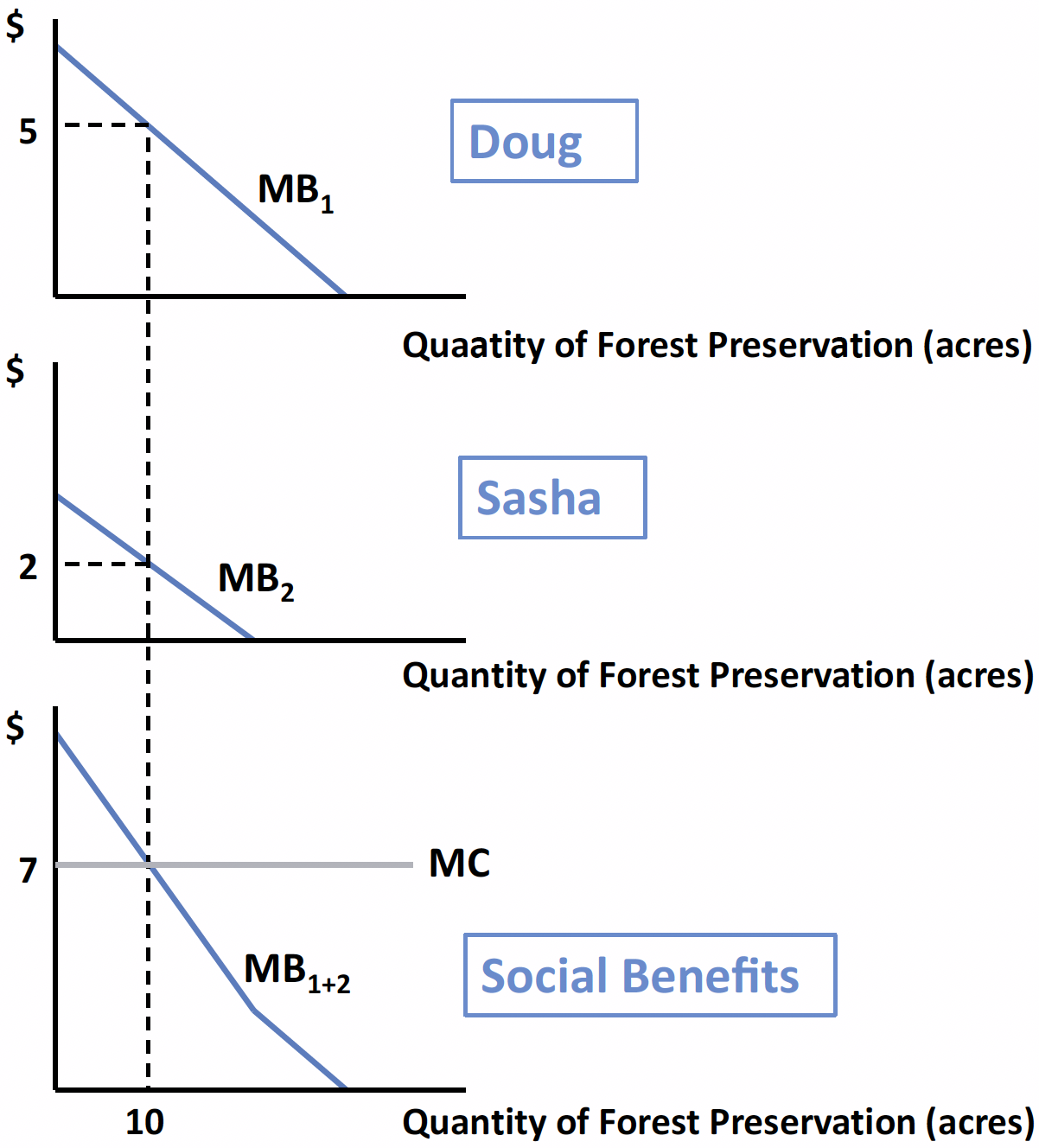
The Economics of Forest Preservation

Imagine two people, Doug and Sasha, who both value forest preservation. Each has a downward-sloping MB curve in acres preserved.

To obtain society’s marginal benefit at quantity \(Q\), add their MBs vertically (because both consume the same public good). If at \(Q=10\) acres Doug’s MB is $5 and Sasha’s is $2, then the social MB at 10 acres is $7.

Assume it costs $7 per acre to preserve land. The efficient quantity is where social MB equals marginal cost: 10 acres (SMB = MC = $7).

Note

The efficient level \(Q^*\) satisfies: \[ \sum_i \text{MB}_i(Q^*) \;=\; \text{MC}(Q^*) \] That is, the sum of individual marginal benefits equals marginal cost.

Why willingness to pay falls short

Even at 10 acres, Doug might be willing to pay only $3 per acre (or nothing), despite receiving $5 of benefit—he still enjoys the forest if others pay. Sasha may understate her value as well. Because there’s no standard market to force truthful revelation, individual payments and true benefits won’t naturally align.

Surveys can help estimate values, but answers may be biased. In practice, public goods decisions require collective processes—elected representatives, direct votes, or community deliberation.

Paying for the efficient level

If 10 acres is optimal and each acre costs $7, total spending is $70. One simple split is $35 each for Doug and Sasha. Doug gets at least $50 of value (10 × $5), so he might accept $35. Sasha, who benefits less, may feel overcharged. This highlights the efficiency–equity tension: choosing the right total quantity is one question; dividing the cost fairly is another.

Scaling to 130 million households with similar patterns implies around $4.5 billion in funding at $35 per household. In reality, benefits and ability to pay differ, so societies debate uniform contributions vs. income-based shares or other formulas. These debates are both political and economic.

References

• Harris J. and Roach B., Chapter 3. Theory of Environmental Externality, Environmental and Natural Resource Economics: A Contemporary Approach (5th Edition)

⚠️ Note: These contents from the above book chapter are shared under fair use for educational purposes to support your learning.

💬 Discussion

Welcome to our Week 6 Discussion Board! 👋

This space is designed for you to engage with your classmates about the material covered in Week 6.

Whether you are looking to delve deeper into the content, share insights, or have questions about the content, this is the perfect place for you.

If you have any specific questions for Byeong-Hak (@bcecon) or peer classmate (@GitHub-Username) regarding the Week 6 materials or need clarification on any points, don’t hesitate to ask here.

Let’s collaborate and learn from each other!